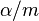Error bars and statistical significance: can we infer the statistical significance of the difference by looking at the error bars of two bar graphs?

Look at the following graph showing the averages and the corresponding error bars. Can we conclude whether the difference between the means of the two groups is statistically significant?

Well, the short answer is yes and no. A longer answer is, if the error bars provide the corresponding 95% confidence interval, the values in these two groups are normally distributed, then the difference is statistically significant at a 5% level using an unpaired t-test.

Now the long answer...

If we are really picky about the terms, we can say that statistical significance depends on the significance level you choose. So the answer of course depends on the level of significance.

Let's choose 5% significance level, which is usually assumed when the significance level is not specified..

The answer? Still not definitive -- because error bars can represent different things. Some people simply plot the standard deviation of the sample, others use them to represent standard errors of the mean, and still others put confidence intervals there. Depending on the nature of the error bars, we may or may not be able to infer the statistical significance of the difference of the mean.

Some words on standard deviation, standard error of the mean, and the confidence interval. Standard deviation simply measures the variability of a data set, without considering the sample size. When the sample size is large enough, it is a good estimate of the population standard deviation. However, when we conduct a statistical test, we are usually investigating whether the means are different in the two groups. In that sense, the standard errors of the means are more informative. 

If data are normally distributed, the standard errors are less than the standard deviation $\sigma$ -- indeed, the standard error of the mean SEM = $\sigma / \sqrt{n}$.  Now as shown below, the standard error bars do not overlap, is the difference between group means statistically significant?

It is hard to tell. However, when we have the error bars represent the 95% confidence intervals, then we can conclude that the difference is statistically significant at 5% if the bars don't overlap. BUT, the opposite is not necessarily true---two 95% confidence intervals that overlap may be significantly different at the 95% confidence level.

                         

What we can tell is whether the sample mean is statistically significant from a specific value by checking whether that value is within the confidence interval or not. For example, the sample mean is significantly different from 0 at 5\% level if and only if 0 is not contained in the 95% confidence interval.

The confidence interval is larger than the standard error bar -- $t_{(1+\alpha)/2}$ times the error bar width, where $t_{(1+\alpha)/2}$ represents the $\frac{1+\alpha}{2}$ quantile of a t-distribution. When the sample size is large, its value is approximately 1.96, which is the quantile for a normal distribution.

Therefore, we can easily conclude whether the difference is statistically significant when the error bars represent confidence intervals. If the error bars represent standard errors of the means, however, we can conclude that the difference is not statistically significant if they overlap.

P.S.: The meaning of a 95% confidence interval? Some people understand it as the population mean of the distribution is in the confidence interval with probability 0.95. Well, that is a wrong interpretation. The mean is a fixed value, it is either in that interval or not, and there is no randomness involved. The correct interpretation? Consider drawing the sample with the same size many times, and each time you have a 95% confidence interval. Then 95% of those confidence intervals (one for each sample) will cover the population mean -- in other words, the population mean falls into 95% of those confidence intervals.

P.P.S.: Sample s1 consists of 19 observations drawn from the normal distribution $N(5, 1^1)$, and sample s2 consists of 100 observations drawn from the normal distribution $N(6,2^2)$.

Mediator vs. Moderator variables

I have a co-author who is a psychologist. As we are collaborating on a paper, I found myself unclear about some of the terms, not just in psychology, but also in statistical analysis. One example is the concepts of mediator (mediating variable) and moderator (moderating variable).

As an economist, these two terms are foreign to me. But after googling them, they can be easily explained in terms of econometrics.

Psychologists use this concept of mediating variable to refer to the underlying psychological factor ($x_m$) that can explain why some external factor ($x_e$) lead to a change in a dependent variable ($y$).
Consider a regression of the dependent variable y on the independent variable $x_e$. If we add $x_m$ to the regression significantly change the direct effect of $x_e$, then $x_m$ can be considered as a mediating variable.





The concept of moderator variables, on the other hand, is closely related to interaction terms in econometrics. When we find that the effect of x1 on y depends on the value of x2, then we call x2 a moderator variable, and it has a moderating effect on the relationship between x1 and y. Moderators are usually categorical variables. Back to the above example, we find altruism x1 influences bidding behavior, but the effect is more pronounced for females. Then here gender x2 is a moderating variable that influences the relationship between altruism x1 and bidding in an all-auction y.

In a regression model,  the relationships between y, x1, and x2 can be expressed as the following relationship:
    $y = b_0 + b_1 x_1 + b_2 (x_1 \times x_2) + \epsilon$

The moderating effect of x2 is measured by b2.

P.S.: Biddings in all-pay auctions provide a measure of competitiveness. The above example is essentially saying that altruistic people are less likely to be competitive, but the effect is more significant for female. In other words, we can say that men seem to care less about the opponent in a competitive environment. How do we measure people's altruism? You can use a dictator game in the lab.

Bonferroni correction

In statistics, the Bonferroni correction is a method used to counteract the problem of multiple comparisons.

Statistical inference logic is based on rejecting the null hypotheses if the likelihood of the observed data under the null hypotheses is low. The problem of multiplicity arises from the fact that as we increase the number of hypotheses being tested, we also increase the likelihood of a rare event, and therefore, the likelihood of incorrectly rejecting a null hypothesis (i.e., make a Type I error).

The Bonferroni correction is based on the idea that if an experimenter is testing  hypotheses, then one way of maintaining the familywise error rate (FWER) is to test each individual hypothesis at a statistical significance level of  times what it would be if only one hypothesis were tested.

So, if the desired significance level for the whole family of tests should be (at most) , then the Bonferroni correction would test each individual hypothesis at a significance level of . For example, if a trial is testing eight hypotheses with a desired , then the Bonferroni correction would test each individual hypothesis at .

https://en.wikipedia.org/wiki/Bonferroni_correction

Norms and Conformity V

Research on social rejection and acceptance finds that our brains treat social threats as seriously as physical threat. It is found in physiology that physical pain is an important mechanism for normal functioning of a human body. The pain people experience makes people retract from harmful situations. It has been observed that people with congenital insensitivity to pain have a shorter lifespan (Nagasako et al., 2003). Children with this condition incur carelessly repeated damage to their tongue, eyes, joints, skin, and muscles.  Some die before adulthood, and others have a reduced life expectancy (Mardy et al., 2001).  Social rejection and the anticipation of it give rise to negative physical sensation. People who experience social rejection show increased activity in the dorsal anterior cingulate cortex and right anterior insula, the areas of the brain that are involved in the experience of pain (DeWall et al., 2010).

In the experiment conducted by Zhong and Leonardelli (2008), people who recalled being rejected feel the room was significantly colder. The slowing of the heart rate is another physiological symptom of rejection (Moor et al., 2010). Social exclusion also has a harmful impact on cognitive ability and causes self-defeating behavior. These results suggest that our social needs are built upon an existing physiological system that evolved to process physical input from the environment (Eisenberger et al., 2003). Companionship, on the other hand, can reduce the physical symptoms that are related to physical pains (Coan et al., 2006). Positive social contacts can predict physiological well-being as people with more positive social contacts are happier and live longer (Cacioppo and Patrick, 2008).

In the evolutionary process of the human species, it is vital to cooperate with others and rely on the group. Individuals who take social exclusion very seriously have an evolutionary advantage to pass on their genes. Genetically, we are wired to be sensitive to even minor nuance of rejection, just as we are sensitive to physical pains. Therefore, it is clearly that people conform to be liked by other group members, to avoid rejection and to maintain a good standing in the group.

Norms and Conformity IV

Neuroscience suggests human beings have the tendency to spontaneously and unconsciously mirror the behaviors of others when they interact with one another. This phenomenon is the so-called chameleon effect” (Hatfield et al., 1993; Chartrand et al., 1999).  Listening to language, for example, is accompanied by an increase in fMRI activity in the primary motor areas for speech production (Wilson et al., 2004) and in the tongue (Iacoboni, 2007). These findings can be extended to other behaviors that are a part of social exchanges.  It can be conjectured that mimicry is important for social relations and the formation of social norms because people who are more helpful and generous toward others are those who are mimicked in experimental situations (Decety, 2007).

Why do people exhibit this tendency to mimic others? Why do people conform? Most economists consider conforming to normative social influence is irrational. Simon (1990) points out that it is adaptive for individuals to learn social norms from others in a society.  As the best learners of the norms have a survival advantage, people are genetically programmed to learn and conform to social norms (Hoffman 1981; Kameda et al. 2003).

Social psychologists have shown that conforming behavior is not at all irrational. Schachter (1951) conducted an experiment which showed that in a group, people tended to like conformists better than nonconformists. In his experiment, there were three confederates taking one of three roles in a discussion: the modal person took a position that conformed to the average position, the deviate took a position diametrically opposed to the general orientation, and the slider initially took a position that was similar to the deviate’s but gradually slid into a modal conforming position.

The results showed that the person who was liked most was the modal person who conformed to the group norm; the deviate was liked least.  When people make decisions, they always think about the social pressure from others, which provide information to the group members as to how well their actions conform to the established norms. Back in the time of hunter-gatherer society when individual human being was almost helpless when faced with severe natural environment and the attack from other tribes, group membership increased an individual’s chance to survive. Hence evolution bequeaths us as a species the desire to form groups. If group membership increases the likelihood of an individual’s survival, favorable standing in a group gained by conformity to the existing norms is desirable. Therefore, we may have been wired genetically to mimic the behavior of members to keep a good standing in a group. On the other hand, the impetus to avoid social rejections by group members due to nonconformity may also be rooted physiologically in the human species.

Why are we risk averse and risk loving at the same time?

Admit it: we are risk averse. This is evolutionarily advantageous: danger was everywhere back in the jungle, and you'd better choose to play safe to survive.

But interestingly, most people like to gamble. Where there is a small possibility that we get really rich, we are willing to take risk for it. If we think about it, all the entrepreneurs are risk loving -- they are willing to take risk to receive profit. Men are more risk loving than women, which make sense from an evolutionary point of view. It also explains why most entrepreneurs are male. Well, incidentally, the reason why most experts in the world are male is because men are wired in such a way that they can focus on polishing a skill, which is different than they way females are created.

One way to explain this is suing probability weighting -- it has been observed that people tend to over-weigh small chance event: we try very hard, more than necessary, to avoid danger that is extremely unlikely to happen; we also expect extremely unlikely gains to happen more often that they should.

But why? Maybe evolutionary theory is the way to go...

Norms and Conformity III

Social influences play an important role in social interactions. Social psychologists suggest that social influence can be informational or normative. Informational social influence occurs when the need to know what is right. They use others as a source of information. Informational social influence usually results in private acceptance wherein people truly believe in what other people are saying or doing.

Informational social influence has been used by economists to explain herd behavior and information cascade, showing how individual rational action can lead to group irrationality (Banerjee, 1992; Bikhchandani et al., 1992). Normative social influence, on the other hand, occurs because people have the need to be accepted by others. Normative social influence usually leads to public compliance, but not necessarily private acceptance. Normative social influence plays an important role in the functioning of social norms.

Social psychologists suggest that people are prone to social influence even when no other people are present. According to the self-awareness theory, people engage in the introspection process and evaluate and compare their behavior to their internal standards and values (Carver, 2003; Duval and Silvia, 2002). We want to consider ourselves as good, decent, wise, and intelligent individuals, and we want to be like by others. In order to feel good about ourselves, we tend to avoid taking actions that are socially inappropriate and abide by our personal norms. When we internalize social norms as our inner beliefs, we will also actively do what is prescribed by social norms.

Norms and Conformity II

Elster (1989) distinguishes social norms from moral norms, claiming that the former is motivated by the emotion of shame while the latter by the emotion of guilt. Also, as social norms are context dependent, moral norms are typically consequentialist and independent of context. This categorization is not helpful for analysis, as there is a great overlap between moral norms and social norms. It is better to simply distinguish social norms from personal norms, where conformity to social norms is motivated by acceptance of others and conformity to personal norms main aims to be liked by oneself. In this categorization, moral norms can fall into either social norms or personal norms, depending on contexts.

Social norms are different from personal norms. While both personal norms and social norms indicate what sort of behavior is appropriate or inappropriate, prescribed or proscribed, they satisfy different psychological needs. According to the self-determination theory, people have three basic psychological needs: autonomy, competence, and connectedness (Deci and Ryan 2000). Conforming to social norms fulfills the need to feel connected to others, to be liked by others. Abiding to personal norms satisfies the need to feel competent, to be right and to be liked by self. Personal norms are shaped by social norms to some extent, but they do not need to be identical. People may or may not internalize social norms as their personal beliefs. An individual may demonstrate a certain behavior prescribed by social norms, but the overt behavior may be incongruent with her personal beliefs. Under certain circumstances, behavior prescribed by social norms may not be conducive to the survival of individuals, so evolution endows human beings the ability to embrace personal beliefs that to some degree differ from social norms.

The Ik people are a good example to illustrate the possible discrepancy between social norms and personal norms. The Ik people often try to avoid situations where they have to follow a social norm. As documented by Turnbull (1987), it is clear that these hunter-gatherers had the norm of reciprocity, but they tried hard to avoid being a help-receiver. They would repair their leaking roof at night in order to escape offers to help and future responsibilities to repay the favor. They also hunted in a furtive way in order not to share the bounty with people encountered along the way. In the case of the Ik people, nobody is violating the norm, but everybody is trying to avoid situations where they would have to follow it.