Statistical inference logic is based on rejecting the null hypotheses if the likelihood of the observed data under the null hypotheses is low. The problem of multiplicity arises from the fact that as we increase the number of hypotheses being tested, we also increase the likelihood of a rare event, and therefore, the likelihood of incorrectly rejecting a null hypothesis (i.e., make a Type I error).
The Bonferroni correction is based on the idea that if an experimenter is testing 
hypotheses, then one way of maintaining the familywise error rate (FWER) is to test each individual hypothesis at a statistical significance level of 
times what it would be if only one hypothesis were tested.
hypotheses, then one way of maintaining the familywise error rate (FWER) is to test each individual hypothesis at a statistical significance level of times what it would be if only one hypothesis were tested.
So, if the desired significance level for the whole family of tests should be (at most)
, then the Bonferroni correction would test each individual hypothesis at a significance level of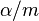
. For example, if a trial is testing eight hypotheses with a desired
, then the Bonferroni correction would test each individual hypothesis at
.
https://en.wikipedia.org/wiki/Bonferroni_correction
No comments:
Post a Comment